Man has ability to find things and best solutions for satisfying own desires but one thing which we never realized and that is our searching power to find anything which is most useful and helpful for us. Whenever we face any problem we do search for best solution. As when we search we got lot of options to solve our problems but we select best one and most of the people says the actual problem arise when we have lot of options and select best one but in Artificial Intelligence Different Searching Algorithms help us to select best choice from many and AI major use in Searching Algorithms. The main theme of this assignment also based on Searching Algorithms of AI. There are four major characteristics to analyze Searching strategy on which base we can say our searching algorithm is best and we got our solution in most efficient manner. Below is the four major characteristics to analyze Searching strategy
Completeness:
The given searching algorithm has ability to complete whole search and give best solution in end.
The given searching algorithm has ability to complete whole search and give best solution in end.
Time Complexity: How much Time will be consumed to get proper solution by following searching technique.
Space Complexity: How much sources will utilize during searching process.
Optimality: Find out best quality solution from many.
Without above mentioned Search strategy we can’t find best Searching Algorithm.
Categories of Searching Strategy
• Uninformed/Blind
• Informed/Heuristic
• Any Path/Non-optimal
• Optimal Path
Q#1: You have to analyze algorithms under blind/uninformed search category i.e. Breadth First Search, Depth First Search, Depth Limited Search and Iterative Deepening. You must have to discuss all four characteristics for each algorithm ONE BY ONE.
Uninformed/Blind search is same like work with blank mind but this also implement using some strategy. In this search there is no proper information about how many steps or path cost required to reached desired goal that’s why it also called Blind search. Six Uninformed search strategies are as follow
• Breadth First Search
• Depth First Search
• Depth Limited Search
• Iterative Deepening Search
• Bidirectional Search
• Uniform Cost Search
1.Breadth First Search:
Breadth First Search is one of the simplest search strategy by expanded the root Node and then generated other nodes from Root in this way got successors. This search can also implemented by calling General Search Algorithm. In this manner a queuing function is used which puts the newly generated states at the end of the queue. This algorithm works at level wise mean level to level goal find and this is best systematic searching technique in which goal can find easily and quickly. This is also time saving because breadth first search always find shallowest goal state first. Now below is the Characteristics of Searching Strategy to see weather Breadth First Search fulfill all four characteristics or not
Completeness: If goal exist in finite depth then terminate.
Time Complexity: Not time saving because as your level of search increasing your time will also increase which will become major headache to solve problem
Space Complexity: Take lot of memory because all the leaf nodes must be maintained in memory
Optimality: Breadth First Search considered good for optimality because if you goal exist in upper level then you can easily find and reached.
2.Depth First Search:
In this Blind Search algorithm move from root to left most successors node. It is best use of memory because it store only one path from root to leaf node. If goal not find then move to siblings if they exist but with same strategy to move left node/link. One of the most important thing which should be follow when applying this strategy, already visited/explore or write node will not visited again so best way is to discard all visited nodes. In many Problems searching Depth First Search considered faster than Breadth First Search because it uses best technique by exploring small portion of whole tree for finding solution.
Completeness: Completeness effect in two ways if the desired goal gain at shallowest level then terminate otherwise the searching continue and in big tree structure its most difficult. So in short its not Complete.
Time Complexity: Depth First Search take less time because in this technique specific path follow instead of flowing whole tree and just move downward so less time required.
Space Complexity: Best use of resources because in this technique on root to leaf node path is saved and if goal not found then visited nodes will discard so it is modest way to use memory.
Optimality: One of the major drawback of depth first search is that it may get stuck on different states because if goal not found and control move deep to deep node then its difficult to find goal because you away from real goal as the real goal may exist at upper level so in this way it is not optimal.
3.Depth Limited Search:
This searching algorithm works same like Depth First search as its time and space complexity is same like Depth first search but with little modification as its name suggest Limited search and this can be done through general search algorithm. As is already discussed in DFS the goal can’t find if searches down with infinite length tree so in this way DFS not guaranteed to find the solution that’s why it not fulfill the characteristic of Completeness so for solving this problem of DFS introduced DLS. DLS guaranteed to find solution with in given depth limit but its not sure to find most optimal path so its not optimal.
Completeness: It is complete search strategy.
Time Complexity: Just move root to leaf so easy take less time as compared to others searching algorithms.
Space Complexity: Less space required no need to store extra nodes which visited already.
Optimality : Not optimal
4.Iterative Deepening Search
Iterative Deepening Search is the combination of Depth First Search and Breadth First Search. In short this combine the best part of both algorithms like IDS is complete and optimal like Breadth First Search with use of less memory like Depth First Search. If take its time then its not better than Breadth First Search because if goal not found then nodes expanded on each low level. Iterative Deepening is the best search technique work in large search space with unknown depth solution.
Completeness: yes! Follow BFS best technique so it is complete searching algorithm. So when goal achieved terminate
Time Complexity: Its not time saving in other words its most worse than BFS in matter of time.
Space Complexity: Use less space by using technique of DFS.
Optimality : yes! Find goal by using best technique so it become easy to reach desired goal by searching best method
Q#2: Compare these algorithms with each other and discuss with reasons/examples that which algorithm is better then other and in what situations/environments.
The above mentioned searching algorithms in Answer 1 has some special characteristics which make them differ from each other. Some algorithms are best in some environment and some are best in other environment these both depend on their characteristics. According to the above discussed unique characteristics of four searching algorithms we can compare them. These algorithms compare according to Characteristics of searching strategy which are completeness, time complexity, space complexity and optimality.
Breadth First Search & Depth First Search
These both are most important and simple in implementation Uninformed/Blind search algorithms and both has opposite characteristics. If we discuss according to their performance and faster searching then BFS said to be faster because it uses shallowest searching technique and works at level wise and on other hand DFS searching to depth so if your goal exist in upper level like Goal may be at level 2 then BFS find it fast and show result but if tree is long then DFS search depth and may b just searching on depth level and got stuck.
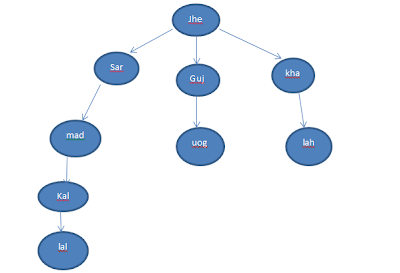
Example 1:
If our Goal is UOG and we move from Jhelum then we have many paths to reach UOG and some may be not take us at UOG so which we select?
If apply BFS then we will got our Goal at level 3 and terminate but if we apply DFS then search start from jhe then sar,mad,kal,lal so its not optimal way to find path.
Depth First Search & Depth Limited Search
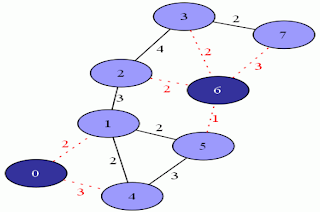
Depth Limited search is use to eliminate the problems of DFS because in DFS goal may not be find if length of tree infinite so with DLS we can overcome from this problem by setting the limit and the search process start and do work until limit value become false. Limit value set according to given problem like in below example Limit value will be l = 3
Example 2:
In the above our Goal is 4 then the DLS works well because in this least one goal state at a depth which less than l, so in this way this algorithm guaranteed to find goal. If apply DFS then that goal move to left most node with depth so its become difficult to reached our goal.
Iterative Deepening Search VS DFS,BFS & DLS
IDS is combine with the best characteristics of DFS and BFS. IDS is basically use to overcome the problem of DLS because in DLS if we don’t have idea about the lowest depth of a goal state then always find the best limit l by trying all possible depths for l until we achieved a goal state. But this technique become wasteful because all the DLS for limit l less than the goal level are not useful and its may be possible many states are expanded many times. So in DLS searching time may be spent at the deepest level of the search tree. So this Searching algorithm works well and in optimal way.
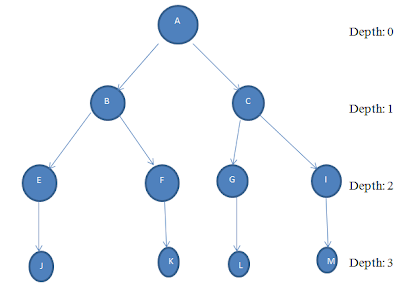
Example 3:
If we assume we don’t have any goal in above example and perform search to find goal that not exist in above example like D so the iteration will be start from Depth 0 where just one start state A which is not the goal so we expand A and got two child B and C as one thing in mind perform DFS and BFS properties and then we see our goal on each depth and expand further in this way our iterations will be
A
ABC
ABEFCGI
ABEJFKCGLIM
In this way whole tree will be searched and it is Complete and Optimal like BFS because all Nodes expanded on each level and it is also modest memory requirements like DFS because just store the result of goal and other visited nodes discard mean not visit again and again.
So now if Compare all Four algorithms in terms of Characteristics of Searching Strategy then result will be
Completeness:
BFS: Goal exist in finite depth then terminate
DFS: Mostly problem searching its not completed and got stuck
DLS: Provide complete search strategy
IDS: Best technique for complete search
Time Complexity:
BFS: Not Time Saving
DFS: Take less time in some situation but most of time also show opposite reaction
DLS: Take less time
IDS: Not time saving because its time complexity equal to BFS
Space Complexity:
BFS: Using lot of memory so not good for resources
DFS: Save lot of memory best for utilizing resources
DLS: Less space required
IDS: Use technique of DFS so less space use
Optimality:
BFS: Provide optimal solution
DFS: Not give optimal solution
DLS: Not optimal for finding solution
IDS: Best! Provide optimal solution
So, in short best one algorithm is IDS but other also best depend on their problem situation as discussed above comparison.
Q#3: Explain how we can improve the performance of all said algorithms?
Before choosing the Searching Algorithm first analyze the problem carefully because without any proper knowledge and understanding about problem we can’t move further and select best searching technique. As in above two questions briefly explain their advantages and disadvantages which gives according to the four basic pillars of searching in AI those are the Characteristics. And the Algorithm which satisfied the maximum characteristics of searching strategy is Iterative Deepening Search. As we can’t break the rules which defined in above four searching algorithms so the best way is to improve their performance is chose best searching algorithm according to problem. Analyze the problem carefully and see which algorithms satisfied maximum characteristics and then apply search.
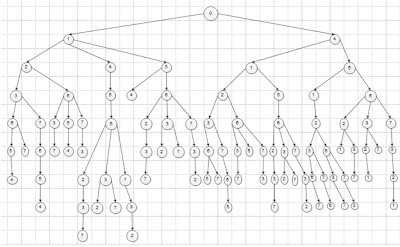
Q#4: Convert following graph in tree and apply Breadth First Search. You have to apply step by step process and show status of OPEN and CLOSE queues.
Answer 4:
Root Node: 0
Goal: 6
Open State | Close State |
Open=[0] | Close=[] |
Open=[1,4] | Close=[0] |
Open=[4,2,4,5] | Close=[1,0] |
Open=[2,4,5,1,5] | Close=[4,1,0] |
Open=[4,5,1,5,3,6] | Close=[2,4,1,0] |
Open=[5,1,5,3,6,5] | Close=[4,2,4,1,0] |
Open=[1,5,3,6,5,4,6] | Close=[5,4,2,4,1,0] |
Open=[5,3,6,5,4,6,2,5] | Close=[1,5,4,2,4,1,0] |
Open=[3,6,5,4,6,2,5,1,6] | Close=[5,1,5,4,2,4,1,0] |
Open=[6,5,4,6,2,5,1,6,6,7] | Close=[3,5,1,5,4,2,4,1,0] |
Open=[5,4,6,2,5,1,6,6,7,3,5,7] | Close=[6,3,5,1,5,4,2,4,1,0] |
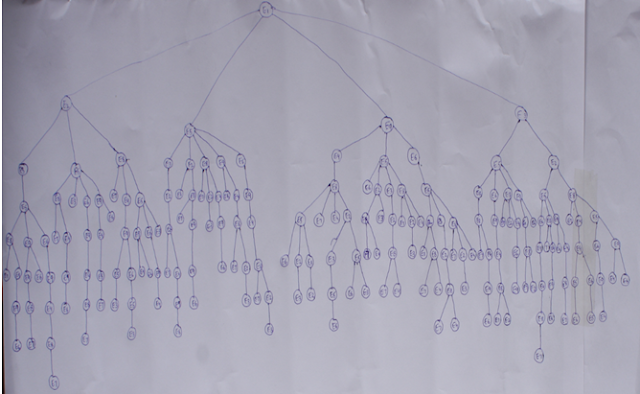
Q#5: Convert following graph in tree and apply Depth First Search. You have to apply step by step process and show status of OPEN and CLOSE queues.
Answer 5:
Directed
Open State | Close State |
Open[E1] | Close[] |
Open[E2,E3,E5,E9] | Close[E1] |
Open[E3,E5,E8,E3,E5,E9] | Close[E2,E1] |
Open[E5,E5,E8,E3,E5,E9] | Close[E3,E2,E1] |
Open[E6,E8,E9,E5,E8,E3,E5,E9] | Close[E5,E3,E2,E1] |
Open[E9,E8,E9,E5,E8,E3,E5,E9] | Close[E6,E5,E3,E2,E1] |
Open[E8,E9,E5,E8,E3,E5,E9] | Close[E9,E6,E5,E3,E2,E1] |
Open[E9,E5,E8,E3,E5,E9] | Close[E8,E9,E6,E5,E3,E2,E1] |
Open[E5,E8,E3,E5,E9] | Close[E9,E8,E9,E6,E5,E3,E2,E1] |
Open[E6,E8,E9,E8,E3,E5,E9] | Close[E5,E9,E8,E9,E6,E5,E3,E2,E1] |
Open[E9,E8,E9,E8,E3,E5,E9] | Close[E6,E5,E9,E8,E9,E6,E5,E3,E2,E1] |
Open[E8,E9,E8,E3,E5,E9] | Close[E9,E6,E5,E9,E8,E9,E6,E5,E3,E2,E1] |
Open[E9,E8,E3,E5,E9] | Close[E8,E9,E6,E5,E9,E8,E9,E6,E5,E3,E2,E1] |
Open[E8,E3,E5,E9] | Close[E9,E8,E9,E6,E5,E9,E8,E9,E6,E5,E3,E2,E1] |
Open[E3,E5,E9] | Close[E8,E9,E8,E9,E6,E5,E9,E8,E9,E6,E5,E3,E2,E1] |
Open[E5,E5,E9] | Close[E3,E8,E9,E8,E9,E6,E5,E9,E8,E9,E6,E5,E3,E2,E1] |
Open[E6,E8,E9,E5,E9] | Close[,E5,E3,E8,E9,E8,E9,E6,E5,E9,E8,E9,E6,E5,E3,E2,E1] |
Open[E9,E8,E9,E5,E9] | Close[E6,E5,E3,E8,E9,E8,E9,E6,E5,E9,E8,E9,E6,E5,E3,E2,E1] |
Open[E8,E9,E5,E9] | Close[,E9,E6,E5,E3,E8,E9,E8,E9,E6,E5,E9,E8,E9,E6,E5,E3,E2,E1] |
Open[E9,E5,E9] | Close[,E8,E9,E6,E5,E3,E8,E9,E8,E9,E6,E5,E9,E8,E9,E6,E5,E3,E2,E1] |
Open[E5,E9] | Close[,E9,E8,E9,E6,E5,E3,E8,E9,E8,E9,E6,E5,E9,E8,E9,E6,E5,E3,E2,E1] |
Open[E6,E8,E9,E9] | Close[,E5,E9,E8,E9,E6,E5,E3,E8,E9,E8,E9,E6,E5,E9,E8,E9,E6,E5,E3,E2,E1] |
Open[E9E8E9E9] | Close[E6,E5,E9,E8,E9,E6,E5,E3,E8,E9,E8,E9,E6,E5,E9,E8,E9,E6,E5,E3,E2,E1] |
Open[E8,E9,E9] | Close[E9,E6,E5,E9,E8,E9,E6,E5,E3,E8,E9,E8,E9,E6,E5,E9,E8,E9,E6,E5,E3,E2,E1] |
Open[E9,E9] | Close[E8,E9,E6,E5,E9,E8,E9,E6,E5,E3,E8,E9,E8,E9,E6,E5,E9,E8,E9,E6,E5,E3,E2,E1] |
Open[E9] | Close[E9,E8,E9,E6,E5,E9,E8,E9,E6,E5,E3,E8,E9,E8,E9,E6,E5,E9,E8,E9,E6,E5,E3,E2,E1] |
Open[] | Close[E9,E9,E8,E9,E6,E5,E9,E8,E9,E6,E5,E3,E8,E9,E8,E9,E6,E5,E9,E8,E9,E6,E5,E3,E2,E1] |
Undirected:
As it has lot of branches so it has lot of Open[] and Close[]







Nice information, Thank you for give us this helpful information.
ReplyDeleteสมัครสมาชิก igoal